closed by Vikash Kumar Solve the following pair of linear equations graphically x 3y = 6, 2x 3y = 12 Also shade the region bounded by the line 2x 3y = 12 and both the coordinate axes pair of linear equations in two variables cbseXy=6 xy=4 How do I solve this system so I can graph itYou only need 2 points to graph a linex y = 6 Let x = 0, then y = 6, giving you (0,6) Let y = 9, then x = 6, giving you (6,0) Plot those 2 points and draw a line thru them ===== xy = 4 Let x = 0, then y = 4, giving you (0,4) Let y = 0, then x = 4, giving you (4,0) Plot thoseQ 1 Solve each of the following system of equations graphically and find the vertices and area of the triangle formed by these lines and the y axis 4x−y−4=0, 3x2y−14=0 Mathematics Q 2 If sec4A=cosec(A−15o), where 4A is an acute angle, find the value of A
Ex 6 3 6 Solve Graphically X Y 6 X Y 4 Teachoo
Solve graphically x y=6 x-y=2
Solve graphically x y=6 x-y=2-2y ≤ x 6 Divide both sides by 2;SolutionShow Solution Consider the line whose equation is x 2y ≤ 6 To find the points of intersection of this line with the coordinate axes Put y = 0, we get x = 6 ∴ A = (6, 0) is a point on the line Put x = 0, we get 2y = 6, ie y = 3 ∴ B = (0, 3) is another point on the line Draw the line AB joining these points




Solve The Following System Of Equations Graphically X Y 6 X Y 2
A System of those two equations can be solved (find where they intersect), either Graphically (by plotting them both on the Function Grapher and zooming in); Solve Graphically the following simultaneous linear equations 5x7y=13 7x6y=3 Algebra Help 1 Verify that (4, 12) is the solution to the system Show work to justify your answer 2xy=5 5x2y=6 2 Solve the system by graphing State the solution x y =2 2y – x = 10 3 Solve the system by substitution State1 Add Y to both sides of your inequality equation 2 You now have X > Y 3 Since there is no equality in this equation, draw the line for X = Y, but make it a dotted line 4 Pick a point anywhere on the graph that is
Solve by Graphing xy=2 , xy=6 x − y = 2 x y = 2 , x y = 6 x y = 6 Subtract x x from both sides of the equation −y = 2−x y = 2 x xy = 6 x y = 6 Multiply each term in −y = 2−x y = 2 x by −1 1 Tap for more steps Multiply each term in − y = 2 − x y = 2 x by − 1 1A math video lesson on Systems of Two Equations This video solves by graphing y=x2 and x=3 #solvebygraphing #systemsofequations #algebra2Every Month weThe elimination method for solving systems of linear equations uses the addition property of equality You can add the same value to each side of an equation So if you have a system x – 6 = −6 and x y = 8, you can add x y to the left side of the first equation and add 8 to the right side of the equation And since x y = 8, you are adding the same value to each side of the first
Answer (1 of 3) What is the graphical representation of the equation xy>0?Solve the Following Simultaneous Equations Graphically X Y = 6 ;But since you can't see into my head, let's put these equations in the form of y = mx b 2x y = 6 yields y = 2x 6 The y intercept is 6 The slope is 2, which makes the x intercept 3 First vertex = (3,0) 2x y 2 = 0 yields y = 2x 2 The y intercept




Ex 6 2 5 Solve X Y 2 Graphically Chapter 6 Cbse




Solved 1 4 Determine Whether The Differential Equation Is Chegg Com
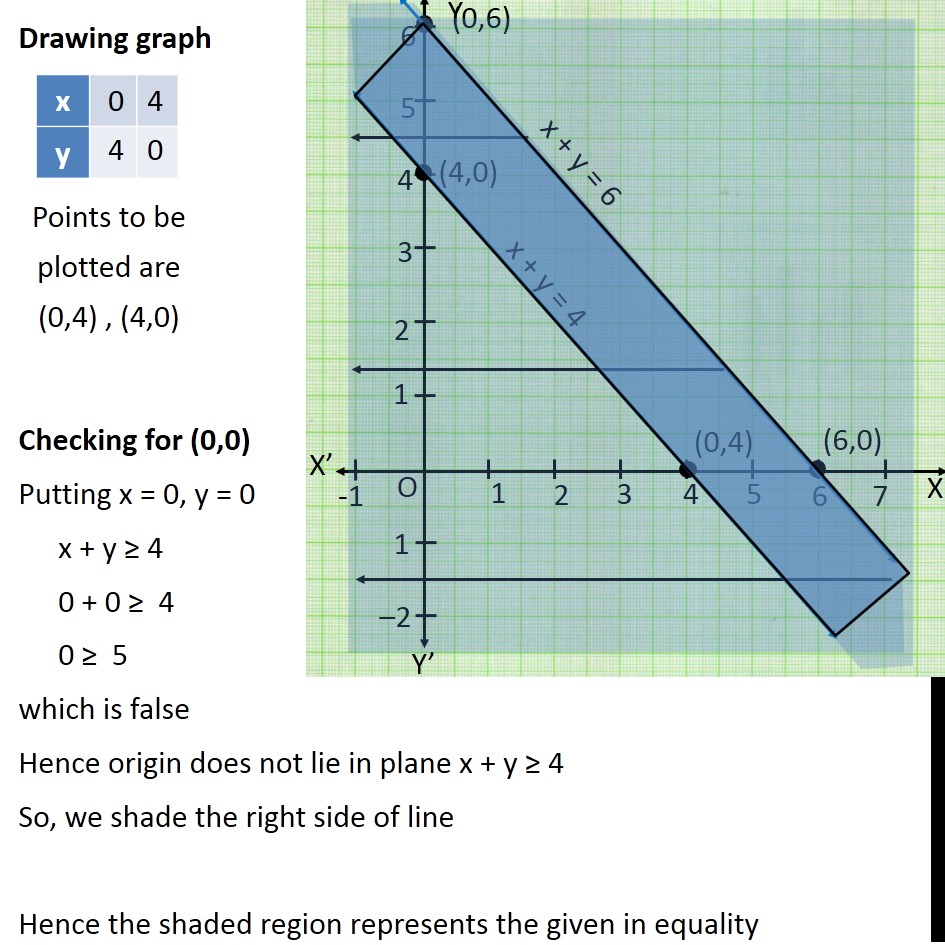
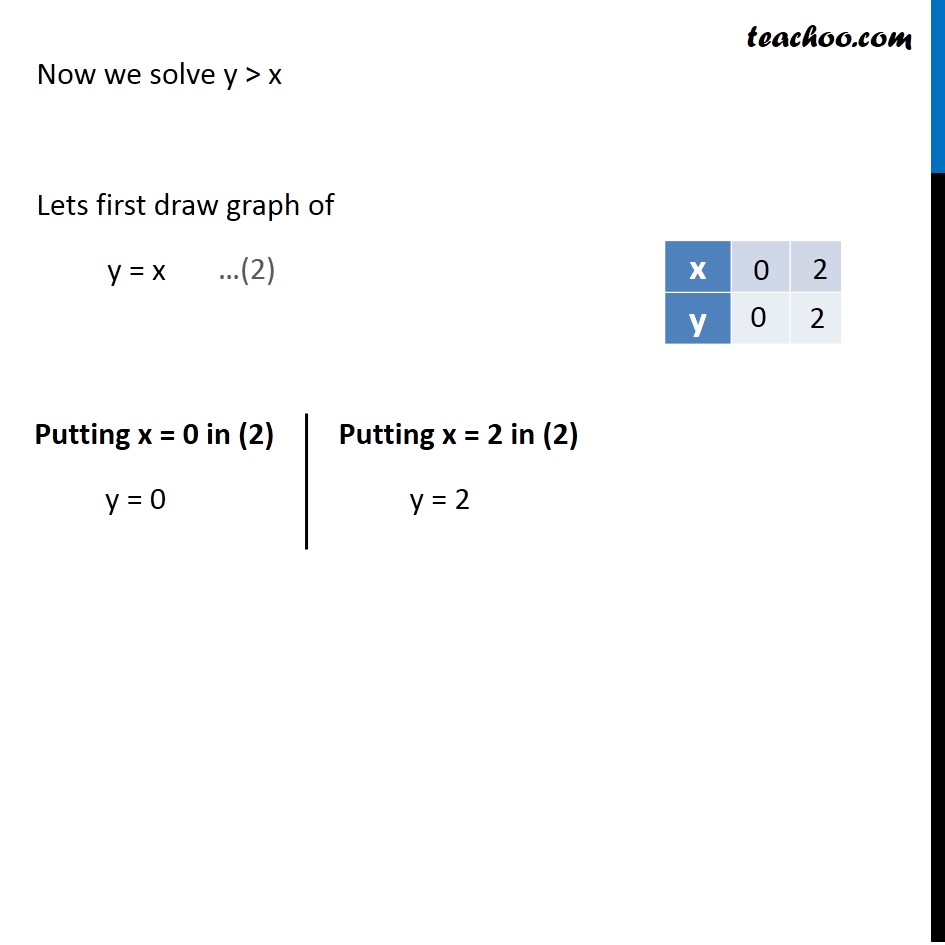
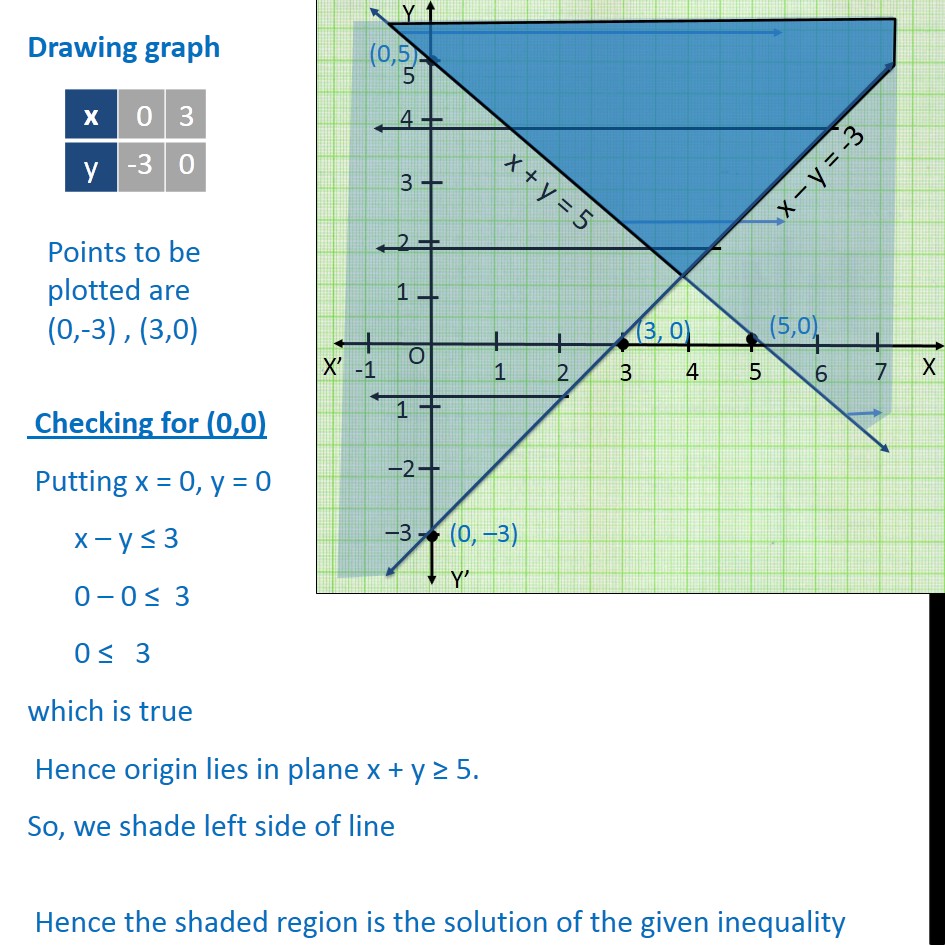
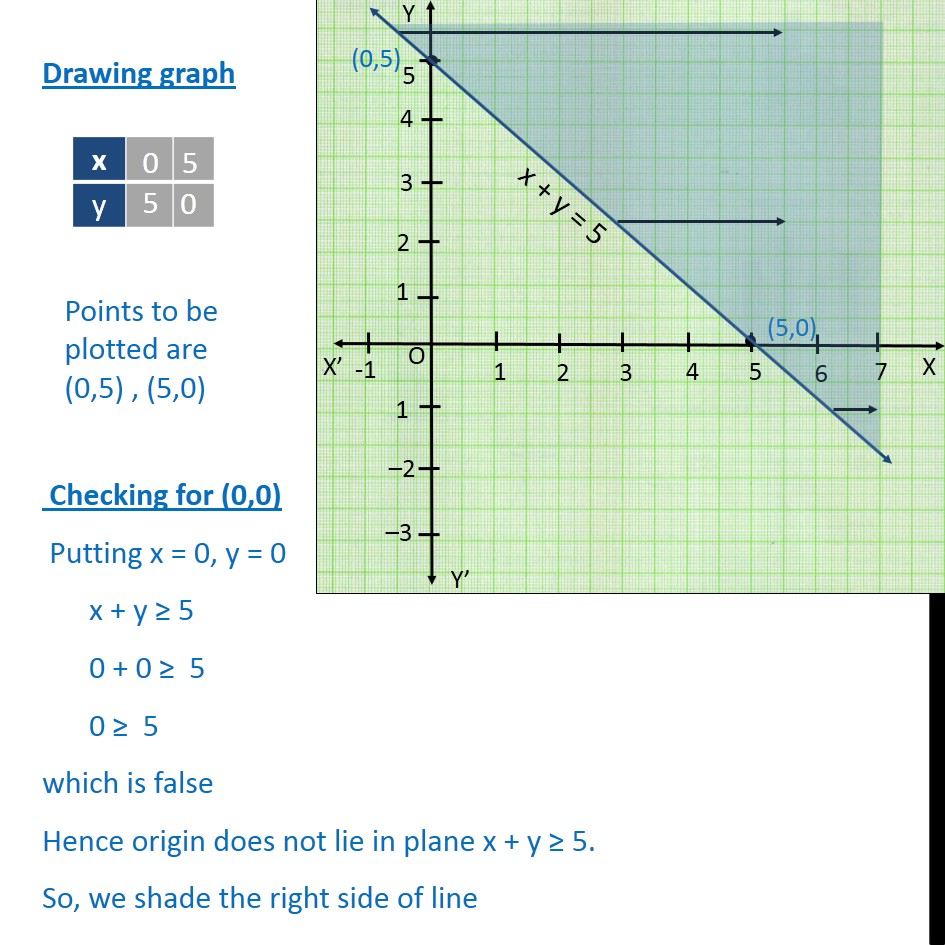
Transcript Ex 63, 6 Solve the following system of inequalities graphically x y ≤ 6, x y ≥ 4 First we solve x y ≤ 6 Lets first draw graph of x y = 6 Putting y = 0 in (1) x 0 = 6 x = 6 Putting x = 0 in (1) 0 y = 6 y = 6 Points to be plotted are (0,6) , (6,0) Drawing graph Checking for (0,0) Putting x = 0, y = 0 x y ≤ 6 0 0 ≤ 6 0 ≤ 6 which is true Hence origin liesSo the second graph, 2y plus 4 equals 6, we put it into slopeintercept form and we graphed it Now, the whole point of this question was to identify the number of solutions that it has, the system A solution to a system of equations is an x and y value that satisfy both of these equationsY = x 2 Find a Central X Value The quadratic equation is y = x 2 − 4x 5, so a = 1, b = −4 and c = 5



Solved 10 8 X Y 14 6 4 X Y 2 2 X 10 8 6 4 N 2 Chegg Com




Solve The Following Simultaneous Equation By Graphical Method X Y 6 X Y 4 Brainly In
2y − x ≤ 6 Solution To graph, this inequality, start by making y the subject of the formula Adding x to both sides gives; For some equation types it can be more than one point and for others, no point at all color(blue)("To determine value of "x) Write as xy=6 ul(xy=2)" "larr" add to and up with only 1 unknown" 2x0=8 Divide both sides by 2 Thus x=4 '~~~~~ color(blue)("To determine value of "y) Substitute x=4 into xy=6" "giving color(brown)(xy=6) " "color(blue)(>" "4y=6) Subtract 4Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Simultaneous Equations Graphically Solve Graphically The System Of Equations



Solve The Following Simultaneous Equations Graphically X Y 2 X Y 4 Algebra Shaalaa Com
Simplify into "= 0" format (like a standard Quadratic Equation)Click here👆to get an answer to your question ️ Solve the given inequalities graphically x 2y≤10, x y≥1, x y≤0, x≥0, y≥0X – Y = 4 Maharashtra State Board SSC (English Medium) 10th Standard Board Exam Question Papers 238 Textbook Solutions MCQ Online Tests 39 Important Solutions 2786 Question Bank Solutions 9112



Ex 6 3 8 Solve X Y 9 Y X X 0 Graphically Ex 6 3
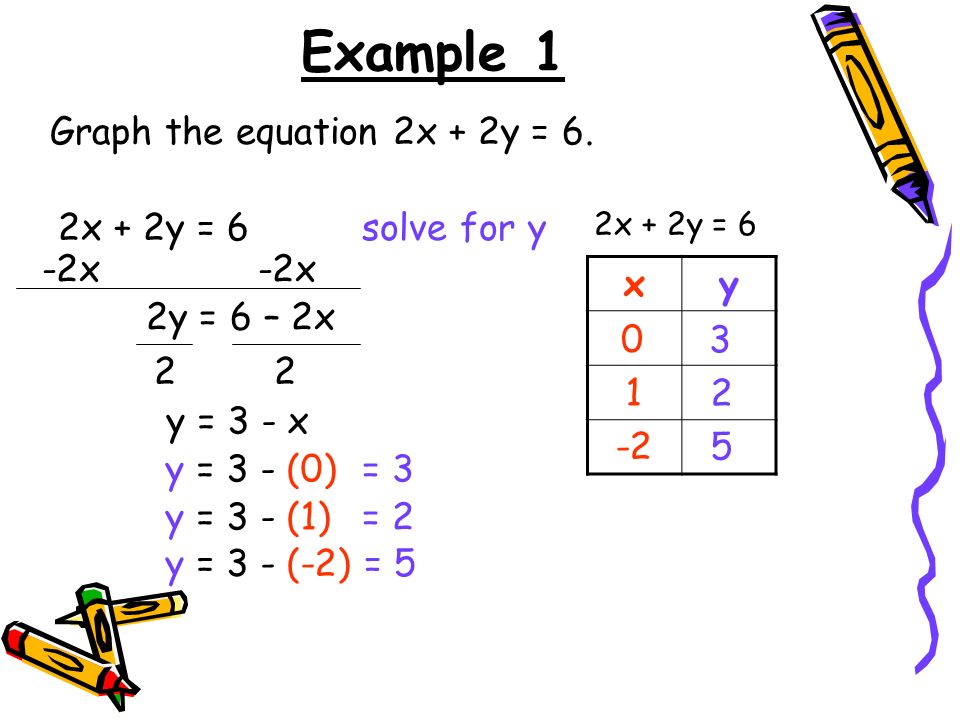



Warm Up 1 Determine Whether The Point 0 3 Is A Solution To Y 5x Minutes 2 Graph Y 2x Ppt Download
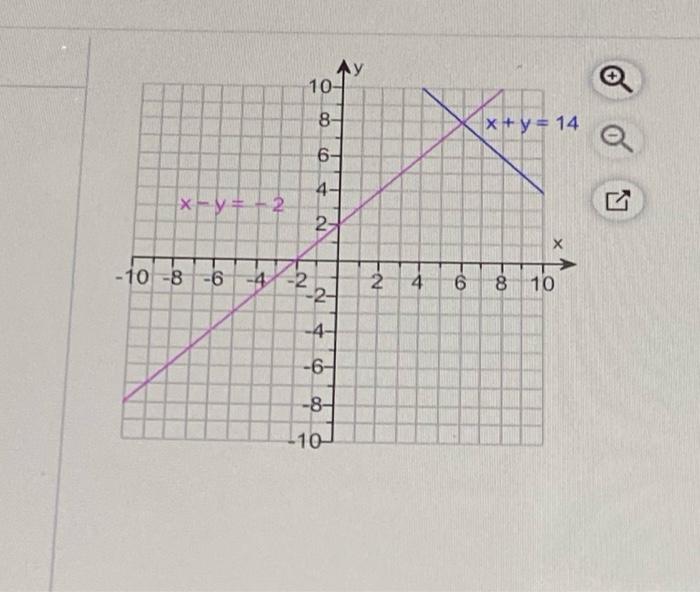
Example 2 Solve graphically the system 6x − 3y = −12 −2x y = 4 Answer Once again, we graph the 2 lines and the intersection point gives the solution for the simultaneous equations 6x − 3y = −12 has xintercept `2`, and yintercept `4`Solve the following systems of equations graphically x y = 6 x y = 2 Solution x = 4, y = 2 Suggest corrections Maths Q4 Solve the following systems of equations x y = 7, y = 6 x and x > y Mathematics Q5 Solve for x and y the following system of equations 5 (x to solve this by graphing we need to remember that the solution to a system of equations is when there is an intersection Step 1 Graph both equations Let (1) xy6=0 (2)xy=0 isolating y from each equation (1) xy6=0 y=x6 to graph a line two points are need, lets find it with x=0 and x=6 y(0)=06 y(0)=6 hence, point 1 = (0,6)




X Y 6 X Y 2 Find X And Y Brainly In



Simultaneous Equations Graphically Solve Graphically The System Of Equations
If the two graphs do not intersect which means that they are parallel then there is no solution Example Using the graphical method, find the solution of the systems of equations y x = 3 y = 4x 2 Solution Draw the two lines graphically and determine the point of intersection from the graph From the graph, the point of intersectionGraph xy=6 Solve for Tap for more steps Subtract from both sides of the equation Multiply each term in by Tap for more steps Multiply each term in by To find the yintercept (s), substitute in for and solve for Solve the equation Tap for more steps Remove parentheses Add and yintercept (s) in point form yintercept Solve by graphing y = \frac{4}{3}x 3 \\y = \frac{2}{3}x 3, find ordered pair, graph and explain x 3y = 2 \\x 2y = 3 Use technology to




Solve The Following System Of Linear Equations Graphically 2x Y 6 0 3x 2y 12 0 Please Give The Brainly In



Solve The Following Simultaneous Equations Graphically I X Y 6 X Y 4 Ii X Y 5 X Y 3 Sarthaks Econnect Largest Online Education Community
Multiply \frac {1} {2} times y6 Multiply 2 1 times − y 6 x=\frac {1} {2}y3 x = − 2 1 y 3 Substitute \frac {y} {2}3 for x in the other equation, 2xy=2 Substitute − 2 y 3 for x in the other equation, 2 x − y = 2 2\left (\frac {1} {2}y3\right)y=2 2 ( − 2 1 y 3) − y = 2Example 4 Graph x y Solution First graph x = y Next check a point not on the line Notice that the graph of the line contains the point (0,0), so we cannot use it as a checkpoint To determine which halfplane is the solution set use any point that is obviously not on the line x = y The point (F U 2 o 0 v 1 N 0 R y K j u z t L a O n S 7 o k f q t Z w Y a h r G e 2 w L M L F C r l Y d A c l g l j S r 1 i V g N h T t d s G l r d e g s s e A r O v C e w d X



Linear Equation Solution Graphically X Y 6 X Y 4 Practice Set 1 2 Q 2 2 Maha State Board Youtube




いろいろ Solve Graphically 2x Y 2 4x Y 8 Solve Graphically 2x Y 2 4x Y 8
Example Solve these two equations graphically to 1 decimal place y = x 2 − 4x 5;X y = 8 (It's the graph that has the two lines intersecting at the top, one is horizontal and the other is diagonal , count across 5 and go up 3) Graph the solution for the following system of inequalities Click on the graph until the correct solution is displayed y ≤ x x y ≥ 1Y=x^21 (Graph Example), 4x2=2 (x6) (Solve Example) Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank you



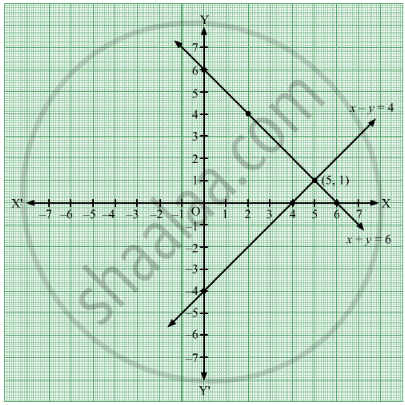
Example 12 Solve X Y 5 X Y 3 Graphically Examples
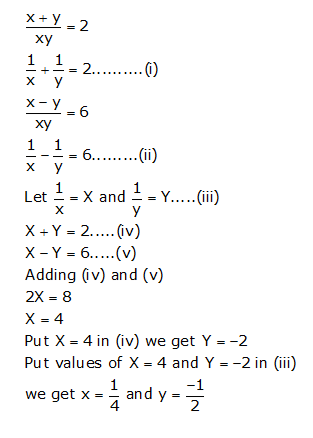



Solve The Following System Of Linear Equations X Y 2 X Y 6 Xy Xy Mathematics Topperlearning Com D9jn35dd
Solve each system by graphing { x = 4 3 x − 2 y = 24 { x = 4 3 x − 2 y = 24 In all the systems of linear equations so far, the lines intersected and the solution was one point In the next two examples, we'll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutionsVideo transcript solve the system of linear equations by graphing and they give us two equations here 5x plus 3y is equal to 7 and 3x minus 2y is equal to 8 when they say solve the system of linear equations they really just saying find an x and a y that satisfies both of these equations and when they say to do it by graphing we're essentiallyGraphically, solve the following pair of equations2x y = 6 and 2x – y 2 = 0 Find the ratio of the areas of the two triangles formed by the lines representing these equations with the xaxis and the lines with the yaxis




Graphical Method X Y 6 X Y 4 Brainly In



How To Solve X Y 7 And X Y 1 Graphically Quora
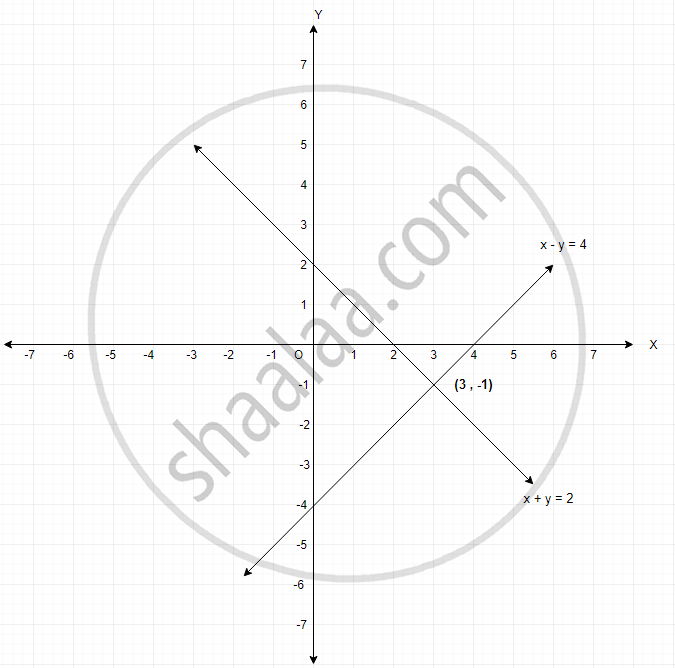
Solve the following system of linear equations graphically 2 x y = 6, x − 2 y 2 = 0 Find the vertices of the triangle formed by the above two lines andHow to Solve using Algebra Make both equations into "y =" format; Ex62, 5 Solve the given inequality graphically in twodimensional plane x – y ≤ 2 x – y ≤ 2 Lets first draw graph of x – y = 2 Drawing graph Checking for (0,0) Putting x = 0, y = 0 x – y ≤ 2 0 – 0 ≤ 2 0 ≤ 2 which is true Hence origin lies in the plane 3x 2y > 6
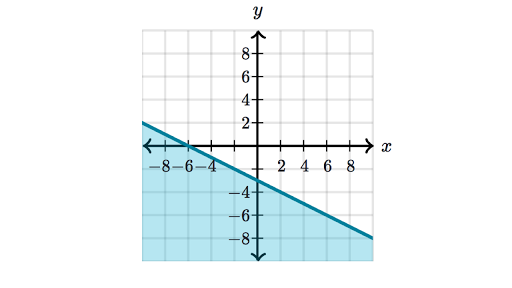



Graphing Inequalities X Y Plane Review Article Khan Academy
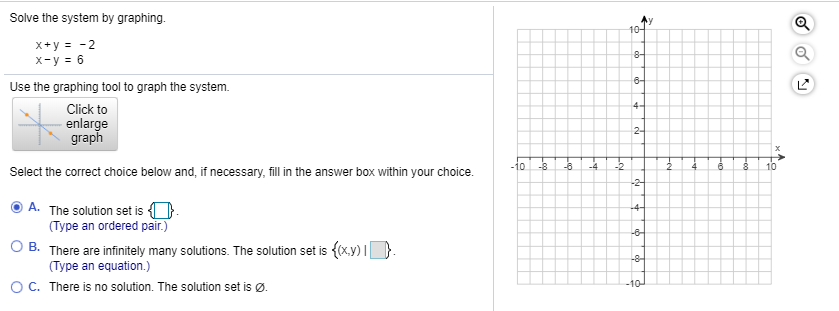



Solved Solve The System By Graphing X Y 2 X Y 6 Use Chegg Com
solve the following system of inequalities graphically 3xy = 10, xy = 6, xy = 2, x = 0, y = 0 Maths Linear InequalitiesSolve the simultaneous equations \(x y = 5\) and \(y = x 1\) using graphs To solve this question, first construct a set of axes, making sure there is enough room to plot the two graphsThe graph of y = 6 x 2 5 x q does not intersect the xaxis Find the range of possible values of q Solution The graph of y = 6 x 2 5 x q does not intersect the xaxis Therefore, Δ < 0 ie 5 2 − 4(6)(q) < 0 25 − 24 q < 0 q > 25 24 ∴ The range of possible values of q is q > 25 24 8 The graph of y = x 2 − 12 x p intersects the xaxis (a) Find the range of possible values of p




Example 12 Solve X Y 5 X Y 3 Graphically Examples




Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Of The Two Triangles Formed By The Lines Representing These Equations With The X Axis And The
Slope is 1/1 = 1 Equation in slopeintercept form y=1*x2 Solved by pluggable solver DESCRIBE 6/1 = 6 TO SOLVE A SYSTEM OF LINEAR EQUATIONS BY GRAPHING Graph the first equation Graph the second equation on the same rectangular coordinate system Determine whether the lines intersect, are parallel, or are the same line Identify the solution to the system If the lines intersect, identify the point of intersectionSet them equal to each other;
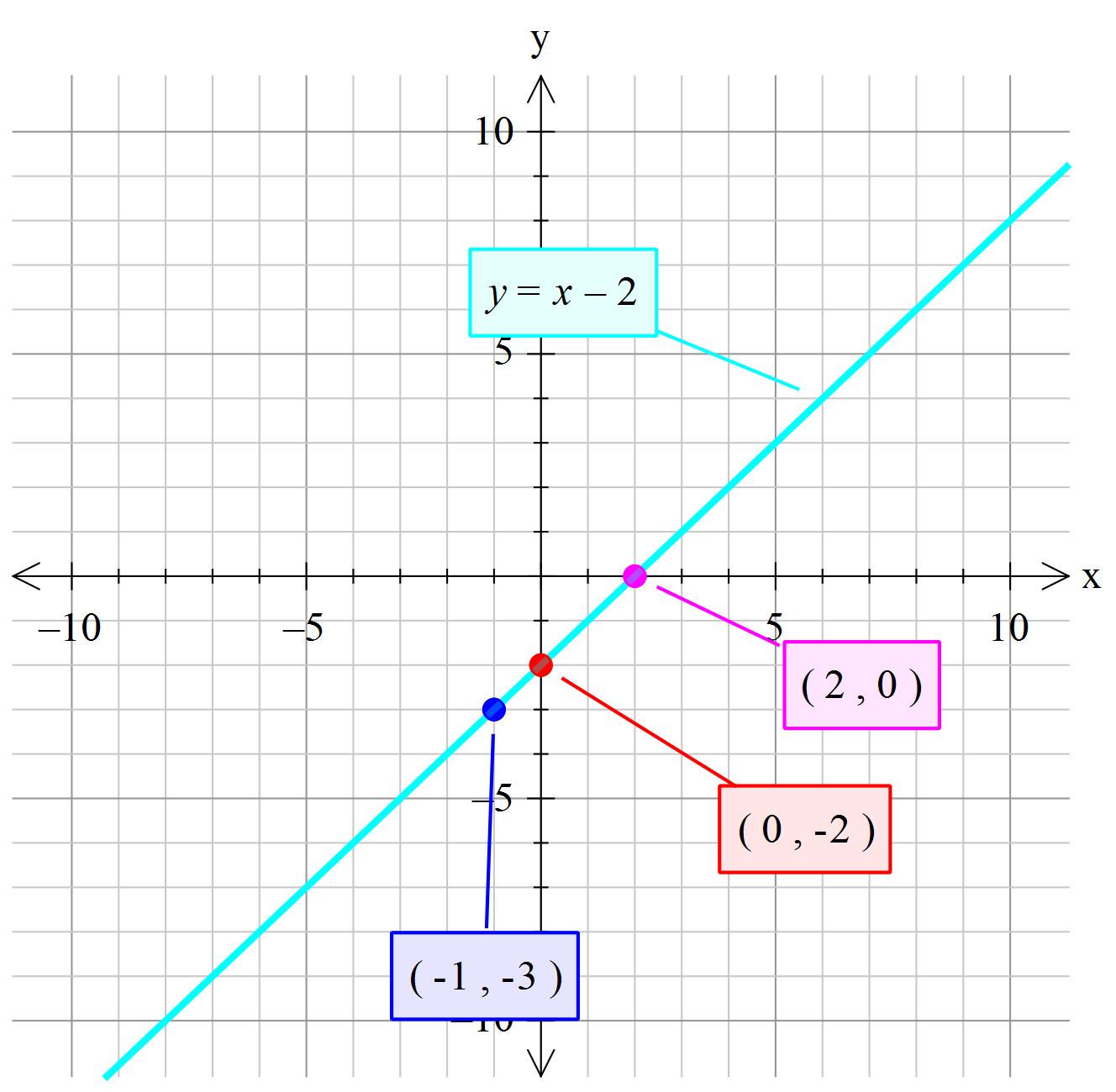



How Do You Graph The Line X Y 2 Socratic




Ex 6 3 6 Solve Graphically X Y 6 X Y 4 Teachoo
We will use 1 and 4 for x If x = 1, y = 2(1) 6 = 4 if x = 4, y = 2(4) 6 = 2 Thus, two solutions of the equation are (1, 4) and (4, 2) Next, we graph these ordered pairs and draw a straight line through the points as shown in the figure We use arrowheads to show that the line extends infinitely far in both directions Now, we plot the points D(0,2), E(1,0) and F(1,4) on the same graph paper We join D,E and F and extend it on the both sides to obtain the graph of the equation 2x y 2 = 0 It is evident from the graph that the two lines intersect at point F(1,4) The area enclosed by the given lines and xaxis is shown in Fig above Answer x=2 and y = 2 Stepbystep explanation Im going to use GeoGebra for graphing the 2 lines I always find it helpful to move y to side of the equation and the rest of the equation to another side This is the slope intercept equation by the way We get our equations as y = 2x6 and y= 2x2 You




Solve The Following Simultaneous Equations Graphically X Y 6 X Y 4




Solve The Following System Of Equations Graphically X Y 6 X Y 2
A math video lesson on Systems of Two Equations This video solves by graphing 4xy=2 and xy=3 #solvebygraphing #systemsofequations #algebra2Every Month wSolve this pair of simultaneous equations graphically y = 2x 1 y = 4x 3 y = 2 x 1 y = 4 x 3 Identify if the equations are linear or quadratic Both the equations are linear This means you will be drawing two straight lines which will intersect at one pointY ≤ x/2 3 Now plot the equation of y = x/2 3 as a solid line because of the ≤ sign The shade below the line because of the ≤ sign




4 4 Solving Simultaneous Equations Equations And Inequalities Siyavula




Ex 6 3 15 Solve Graphically X 2y 10 X Y 1
The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}xy6=0 x 2 x − y − 6 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 1 for b, and 6y for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}X^3 5*x 2*x^2 7 = 0 Now graph the function f(x) = x^3 5*x 2*x^2 7 There are several things to notice about the graph of f 1 The yintercept appears to be (0,7), and in fact these are the exact coordinates The yintercept of the graph of a function is easy to find You simply evaluate the function at 0, and in this example, f(0
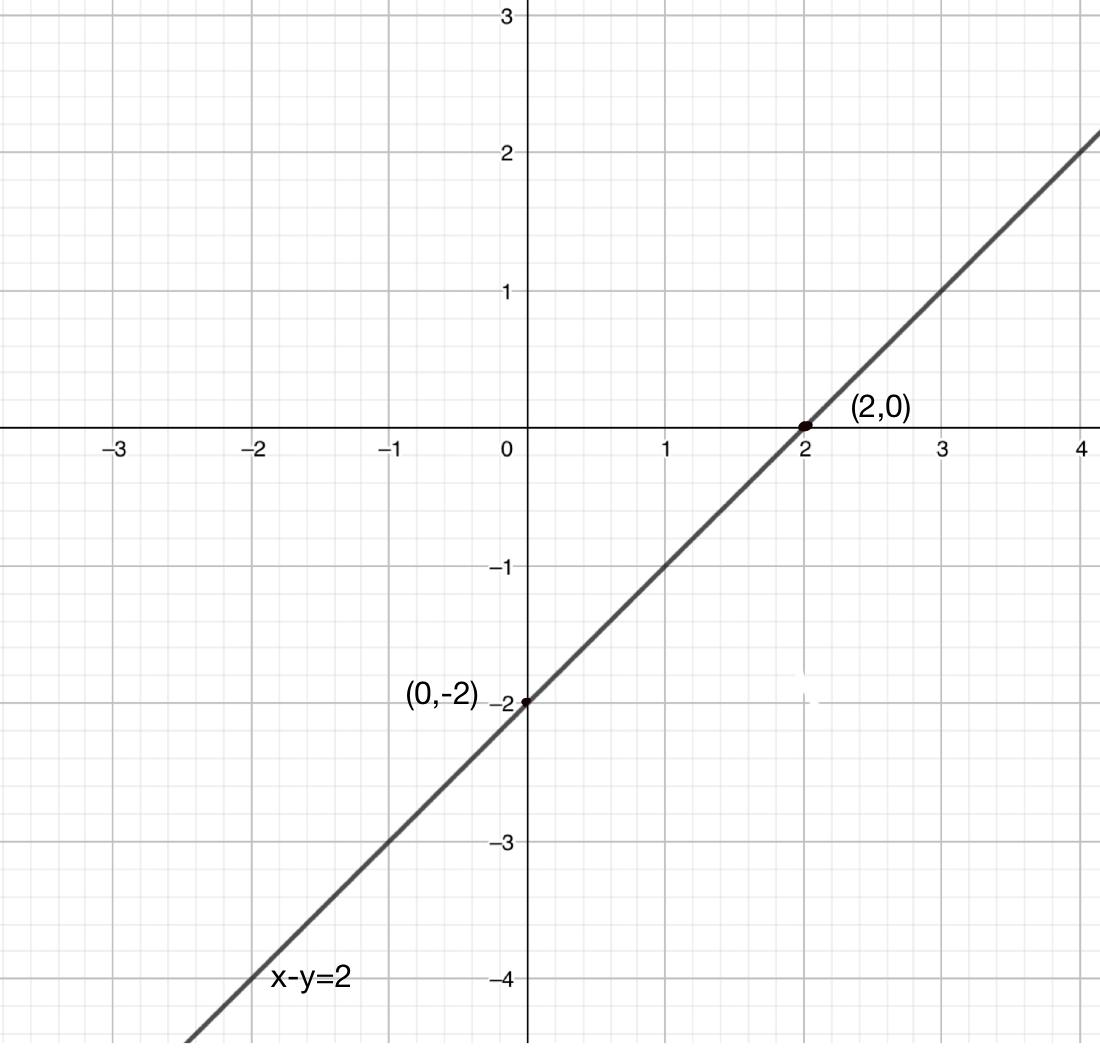



Draw The Graph Of Each Of The Following Linear Equations Class 9 Maths Cbse



Example 12 Solve X Y 5 X Y 3 Graphically Examples




Omtex Classes X Y 6 X Y 4



Simultaneous Equations Graphically




How Do You Solve The System 4x 2y 6 And X Y 3 Socratic




Solve The Given Inequalities Graphically X 2y 10 X Y 1 X Y 0 X 0 Y 0



Equation




Draw The Graph Of The Equation X Y 6 And 2x 3y 16 On The Same Graph Paper Find The Coordinates Of The Brainly In



Solve The Following Simultaneous Equations Graphically X Y 6 X Y 4 Algebra Shaalaa Com



Simultaneous Equations Graphically Solve Graphically The System Of Equations




X Y 6 X Y 4 Practice Set 1 2 Simultaneous Equation Graphically Graph Method Grade 10 Youtube



Systems Of Linear Equations



Solve The Following Simultaneous Equations Graphically I 3x Y 2 0 2x Y 8 Ii 3x Y 10 X Y 2 Sarthaks Econnect Largest Online Education Community




X Y 6 X Y 4 Simultaneous Equation Graphically Brainly In
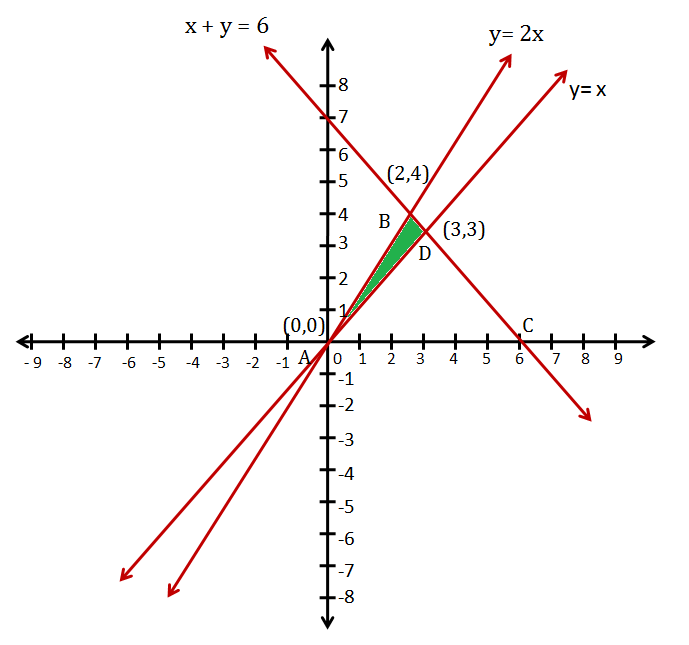



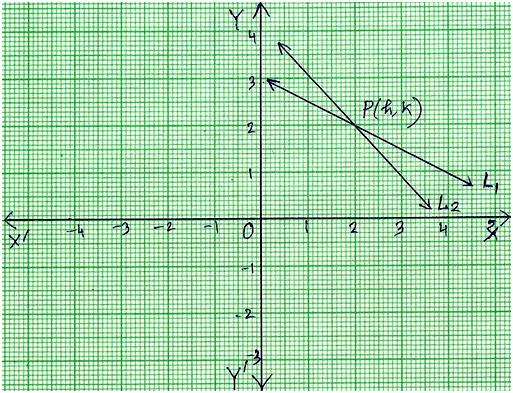
Determine Graphically The Co Ordinates Of The Vertices Of The Triangle Formed By The Equation Whose Sides Are Y X Y 2x X Y 6 Also Area And Co Ordinate Mathematics Topperlearning Com Ee7ugaa
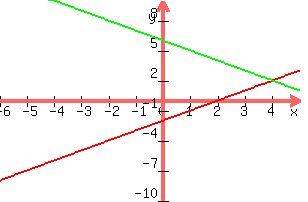



How Do You Solve The System X Y 2 And X Y 6 By Graphing Socratic




Solve The Following System Of Inequalities Graphically 3x Y 10 X Y 6 X Y 2 X Maths Linear Inequalities Meritnation Com
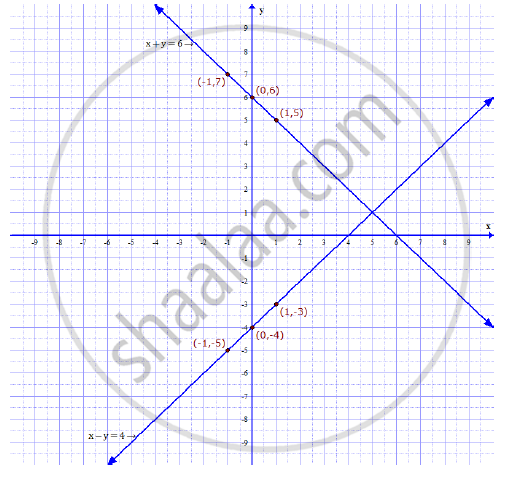



Solve The Following Simultaneous Equations By Using Graphical Method X Y 6 X Y 4 Algebra Shaalaa Com
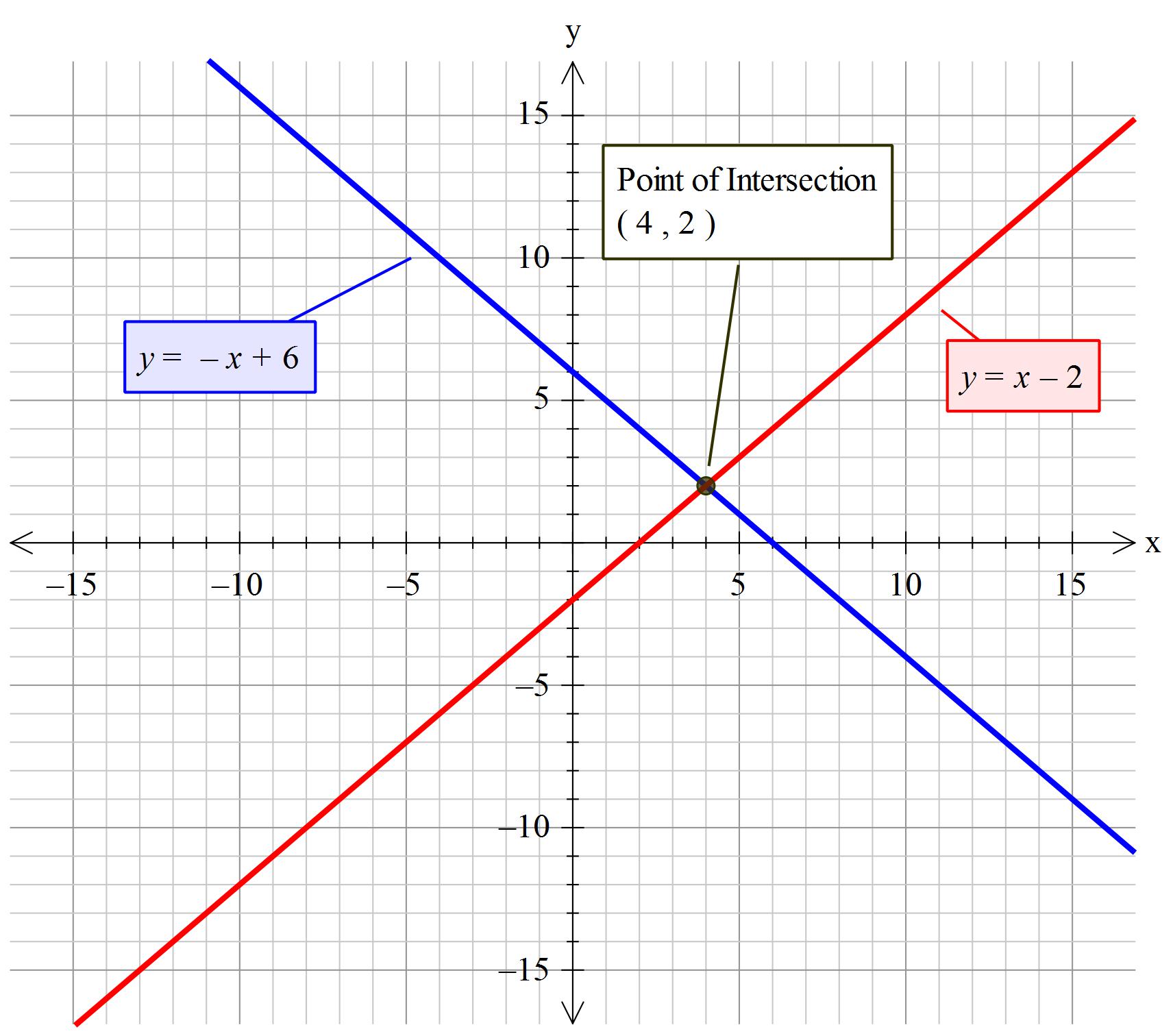



How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic
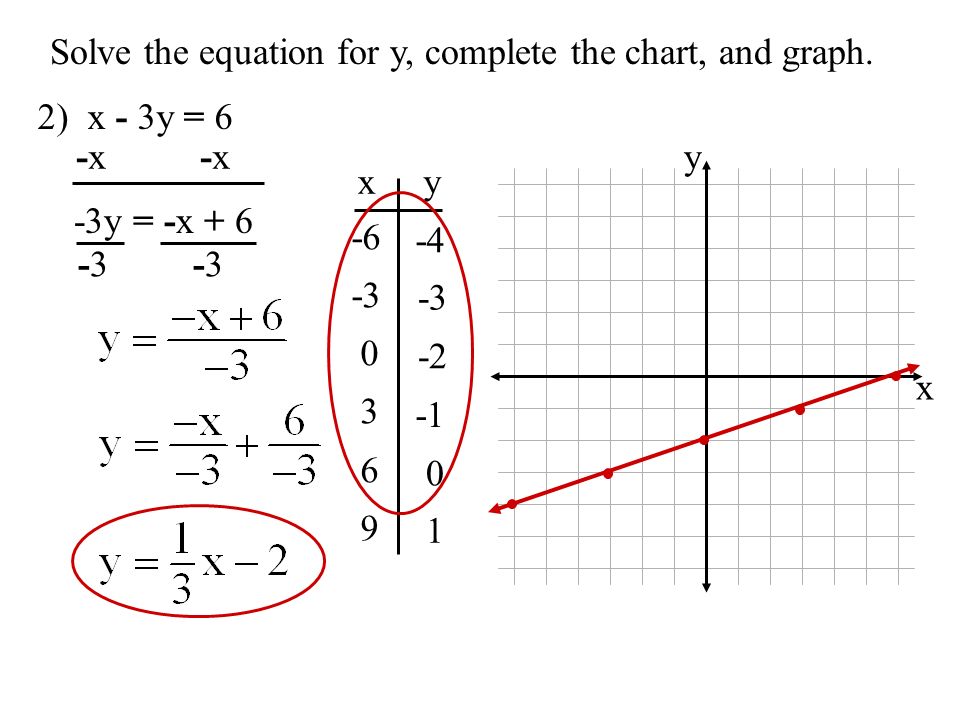



Objective To Graph Linear Equations Using X Y Charts One Variable Equations Two Variable Equations 2x 3 X 14 X 7 One Solution Ppt Download




Solve By Elimination Method X Y 6 X Y 4 Maths Linear Equations In Two Variables Meritnation Com
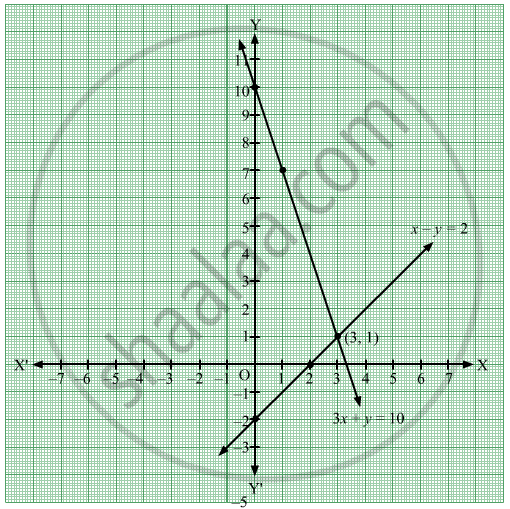



Solve The Following Simultaneous Equation Graphically 3x Y 10 X Y 2 Algebra Shaalaa Com
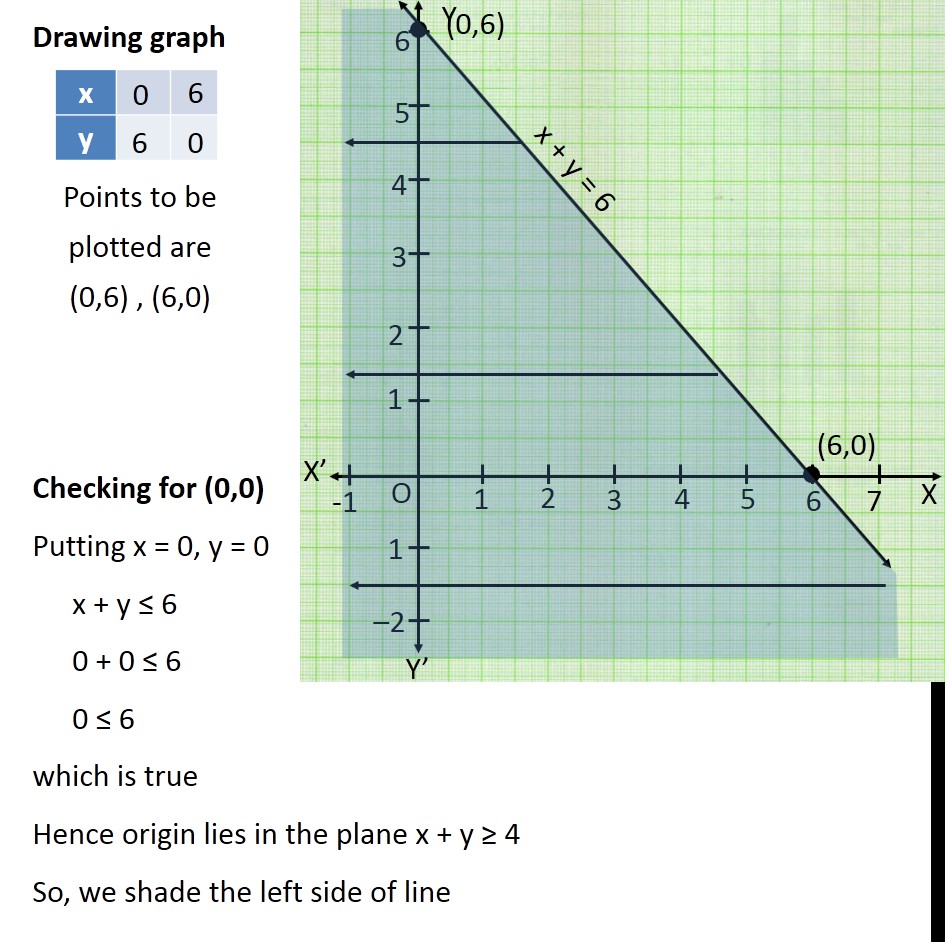



Ex 6 3 6 Solve Graphically X Y 6 X Y 4 Teachoo
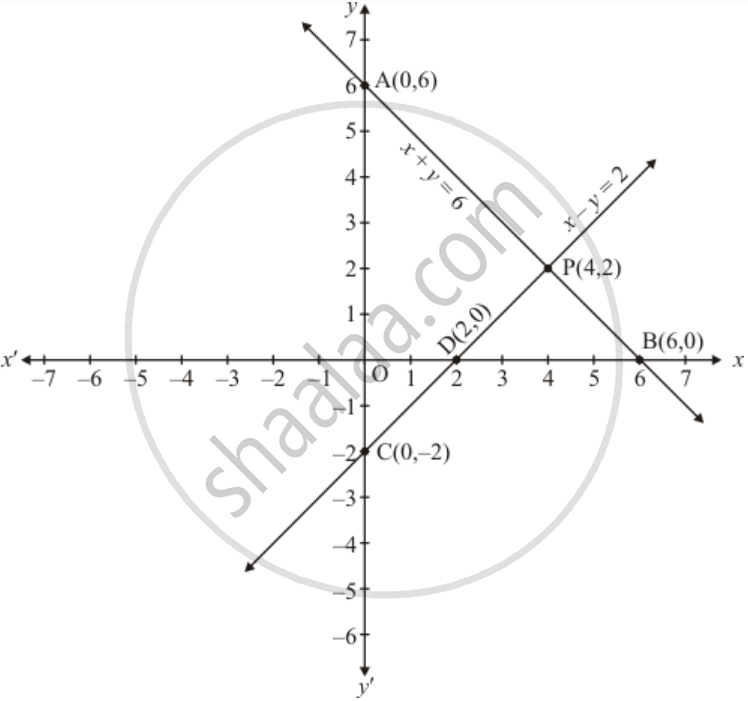



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Mathematics Shaalaa Com




Ex 6 2 2 Solve 2x Y 6 Graphically Chapter 6 Class 11
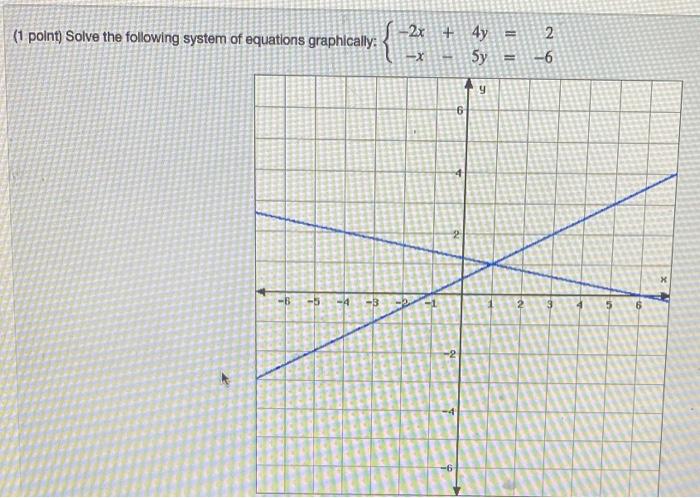



Solved 1 Point Solve The Following System Of Equations Chegg Com



Warm Up Determine If 3 4 Is A Solution To The Equation 1 Y 2x 2 2 6x 3y 6 4 2 3 2 4 6 2 6 3 3 4 6 18 12 6 Yes Ppt Download



Solve The Following Simultaneous Equations Graphically I X Y 6 X Y 4 Ii X Y 5 X Y 3 Sarthaks Econnect Largest Online Education Community



X Y 2 Graph




1 Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Youtube



Solution X Y 10 X Y 2



Solution Solve By Graphing X Y 2 X Y 6




Solve The Following System Of Linear Equations Graphically 2x Y 6 X 2y 2 0 Find The Vertices Of The Triangle Formed By The Above Two



Solution Graph The Equation X Y 6




Solve The Following System Of Linear Equations Graphically 2x Y 6 X 2y 2 0 Find The Area Formed By The Above Two Lines Maths Pair Of Linear Equations In Two Variables Meritnation Com



How Do You Solve The System Of Equations X Y 8 X Y 4 By Graphing Socratic



Solution Solve By Graphing X Y 2 X Y 8 Would It Be 2x 10
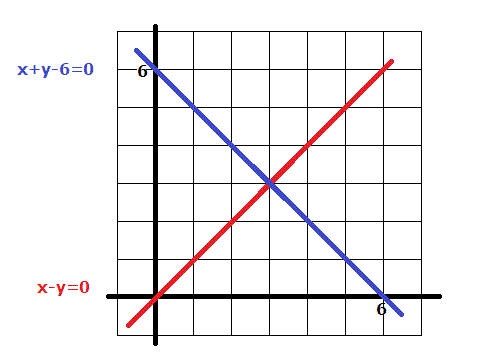



How Do You Solve The System X Y 6 0 And X Y 0 By Graphing Socratic
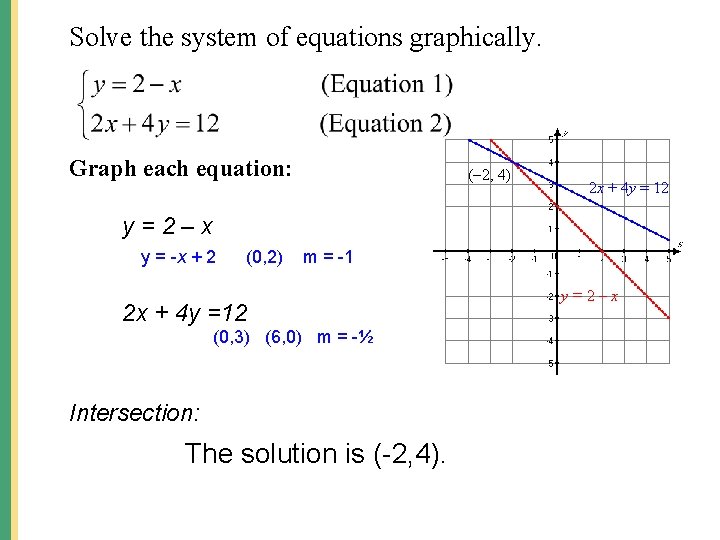



9 1 Solving Systems Of Linear Equations Graphically




Solve The Following Simultaneous Equations Graphically X Y 6 X Y 4




Ex 6 3 6 Solve Graphically X Y 6 X Y 4 Teachoo
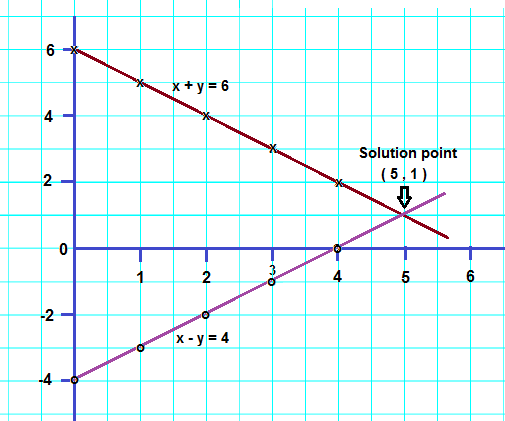



Use Graphical Method X Y 6 X Y 4 Vm9zegrr Mathematics Topperlearning Com




Solved 6 X Y 2 3x 2y 11 This System Of Equations Is Used Chegg Com




Draw The Graph Of Linear Equations X Y 6 And X Y 2 On The Same Graph Paper And Find The Coordinates Of Brainly In



Graphing Systems Of Linear Equations




Omtex Classes X Y 5 X Y 3 Solve The Following Simultaneous Equations Graphically




Solved 6 X Y 2 3x 2y 11 This System Of Equations Is Used Chegg Com




Solve The Equation Graphically X Y 6 3x Y 10 Brainly In
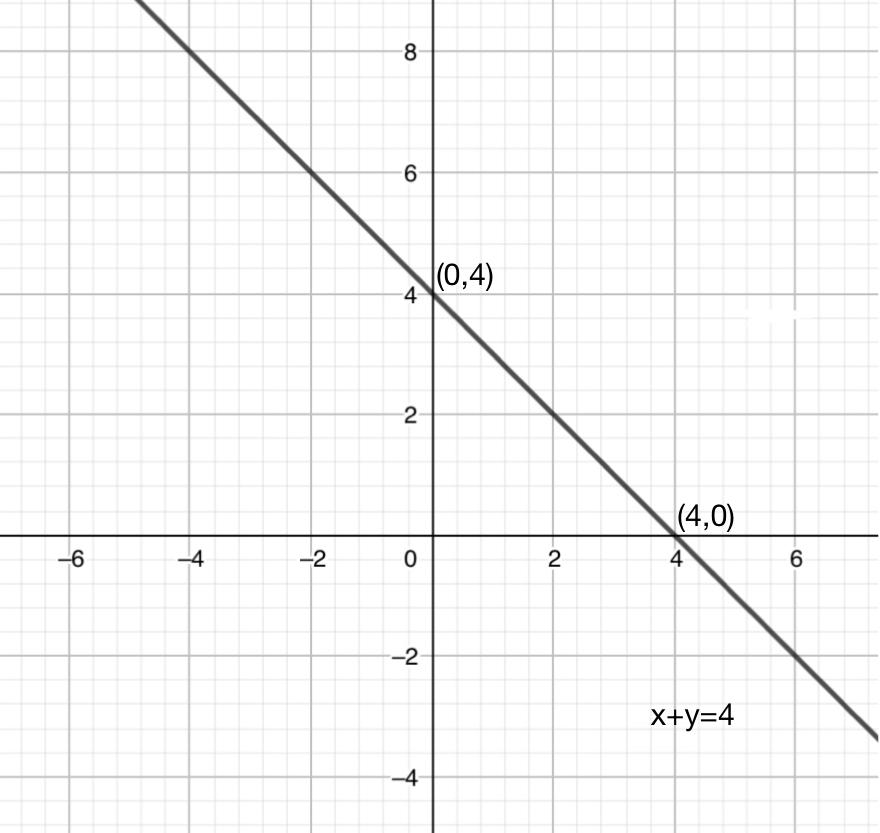



Draw The Graph Of Each Of The Following Linear Equations Class 9 Maths Cbse




Graphically Solve The Following Pair Of Equations 2x Y 6 And 2x Y 2 0 Find The Ratio Of The Areas Youtube



Solve The Following Simultaneous Equations Graphically I X Y 6 X Y 4 Ii X Y 5 X Y 3 Sarthaks Econnect Largest Online Education Community




Omtex Classes X Y 6 X Y 4




Draw The Graph For Each Of The Equation X Y 6 And X Y 2 On The Same Graph Paper And Find The Co Ordinate Maths Linear Equations In Two Variables Meritnation Com




Graphical Method Of Solving Linear Equations In Two Variables A Plus Topper




Q3e 3x Y 10 X Y 2 Solve The Following Simultaneous Equation Graphically
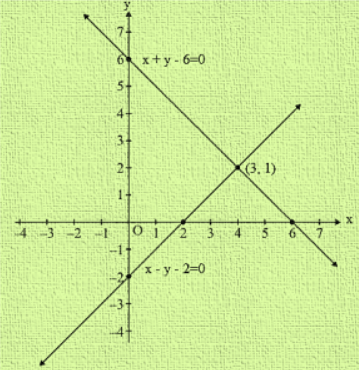



R D Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Sarthaks Econnect Largest Online Education Community
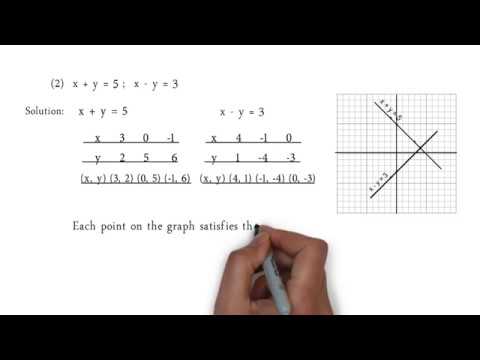



X Y 5 And X Y 3 P S 1 2 Q2 2 Linear Equations In Two Variables Youtube
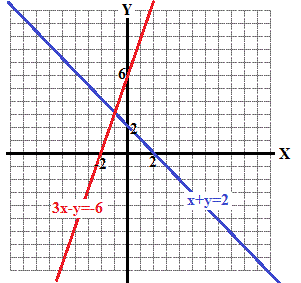



How Do You Solve By Graphing 3x Y 6 And X Y 2 Socratic
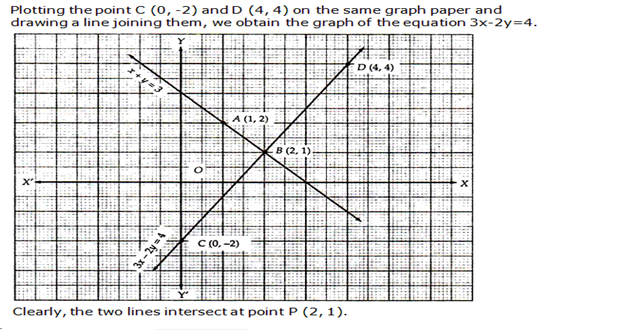



Solve Graphically The System Of Equations X Y 3 3x 2y 4 Mathematics Topperlearning Com Ja91bwemm
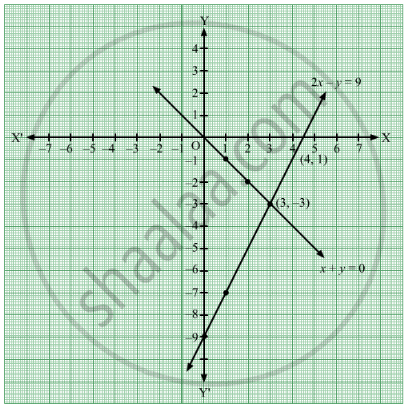



Solve The Following Simultaneous Equations Graphically X Y 0 2x Y 9 Algebra Shaalaa Com




Graphing Inequalities X Y Plane Review Article Khan Academy



Solved Find The Common Solution Of Each Using The Elimination Substitution And Graphical Method 2x Y 2 X 3y 36 2 3x Y 6 X Y 6 3 Course Hero
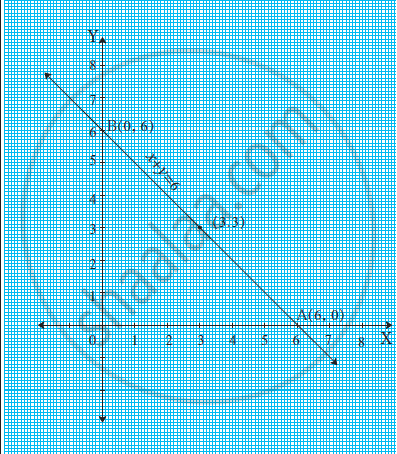



Draw The Graph Of X Y 6 Which Intersects The X Axis And The Y Axis At A And B Respectively Find The Length Of Seg Ab Also Find The Area Of



X Y 6 X Y 2 Graph And Solve Math Homework Answers
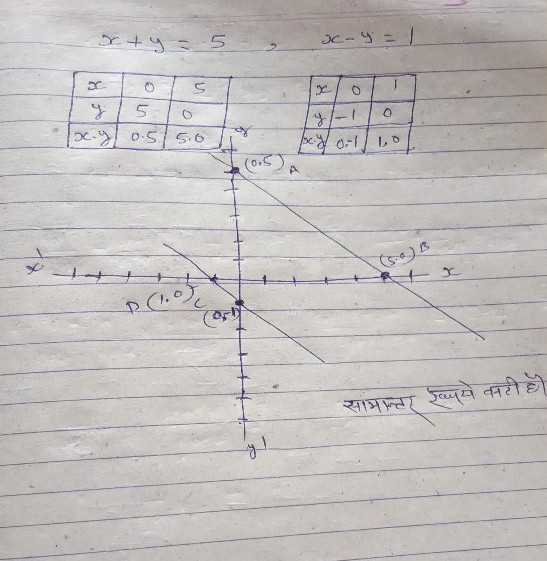



Solve Graphically X Y 5 And X Y 1 Scholr



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Sarthaks Econnect Largest Online Education Community




Draw A Graph X Y 4 And X Y 2 Brainly In
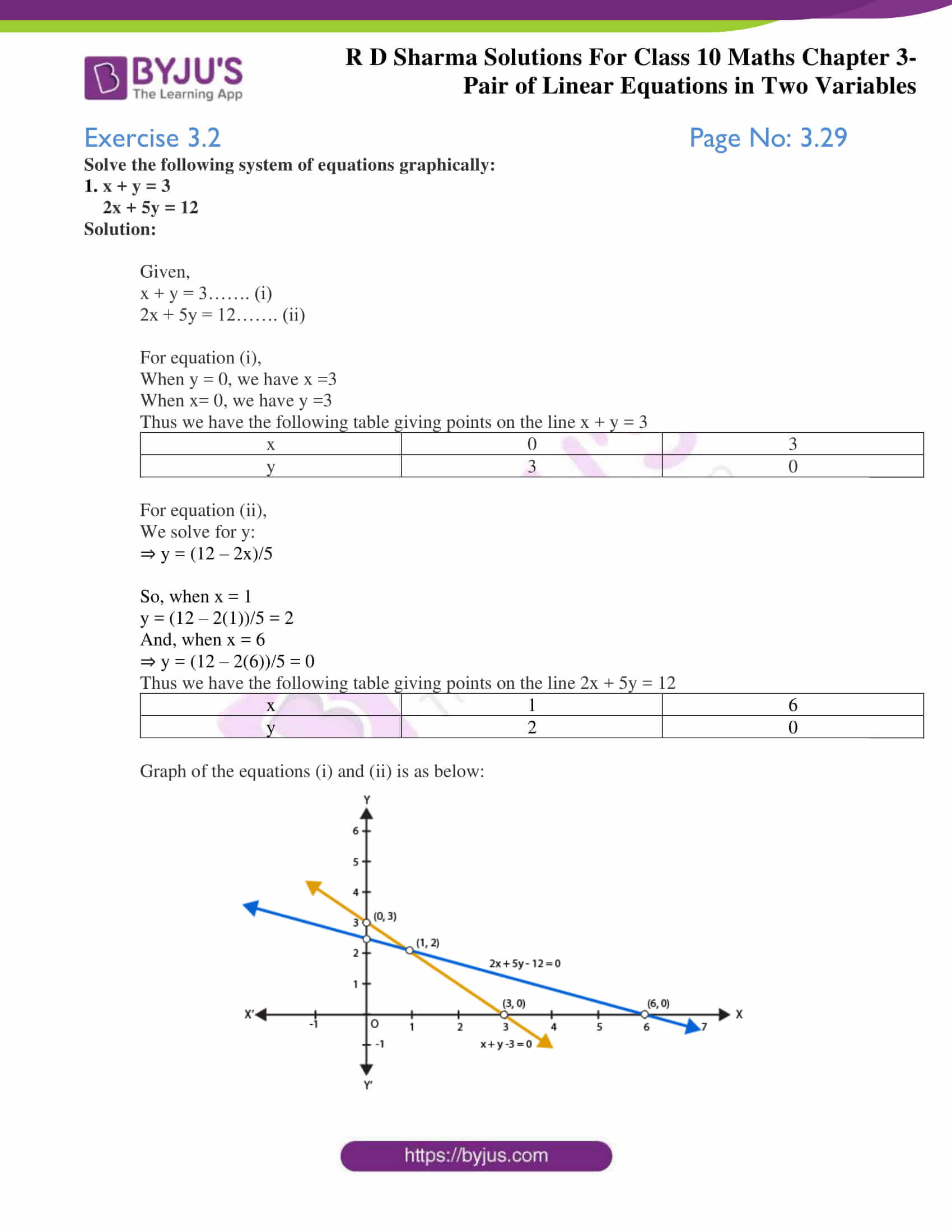



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
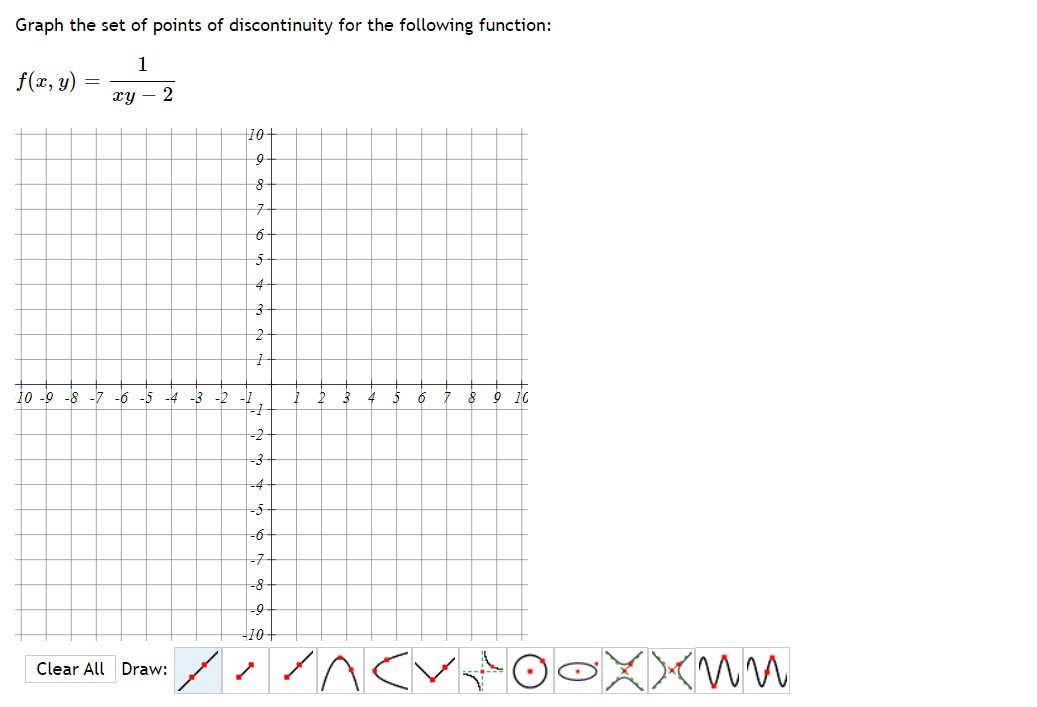



Solved Graph The Set Of Points Of Discontinuity For The Chegg Com




Draw The Graph For Each Of The Equation X Y 6 And X Y 2 On The Same Graph Paper And Find The Coordinates Of The Point Where The Two Straight Lines Intersect




Draw The Graph For Each Of The Equation X Y 6 And X Y 2 On The Graph And Find The Coordinates Of The Maths Linear Equations In Two Variables Meritnation Com
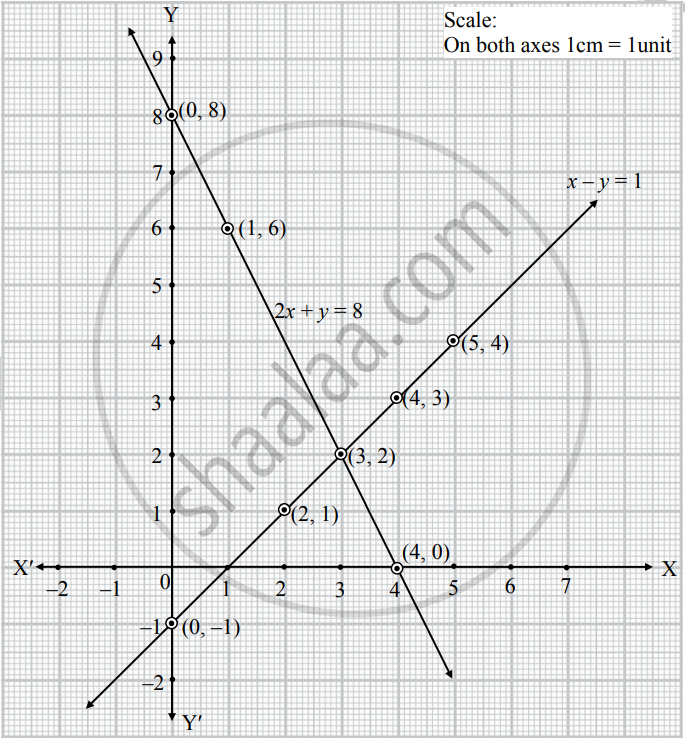



Solve The Following Equations By Graphical Method X Y 1 2x Y 8 Algebra Shaalaa Com
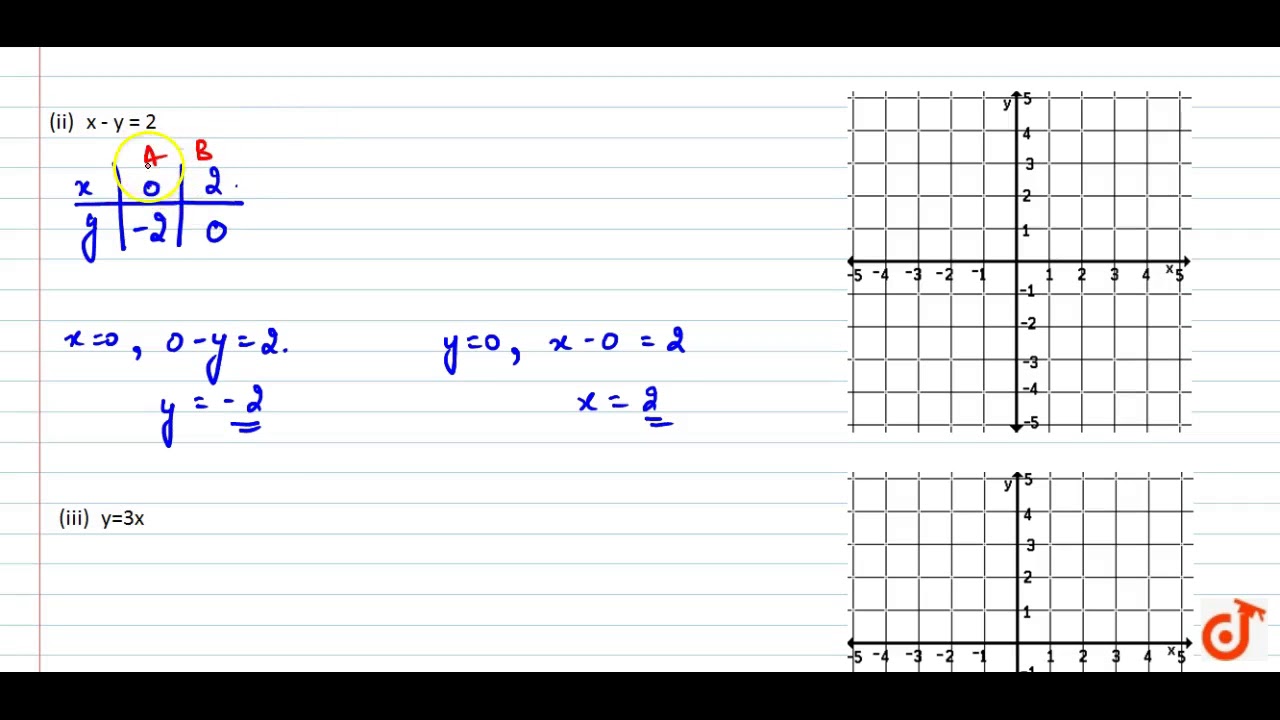



Draw The Graph Of Each Of The Following Linear Equations In Two Variables I X Y 4 Ii X Y Youtube



0 件のコメント:
コメントを投稿